Pneumatic artificial muscle actuator
Review on pneumatic artificial muscle as actuator.
Overview
Pneumatic Artificial Muscle (PAM) actuator is an alternative actuator that mimics muscle mechanism. PAM uses air pressure to change its length, so it can mimic how muscle contracting and relaxing.
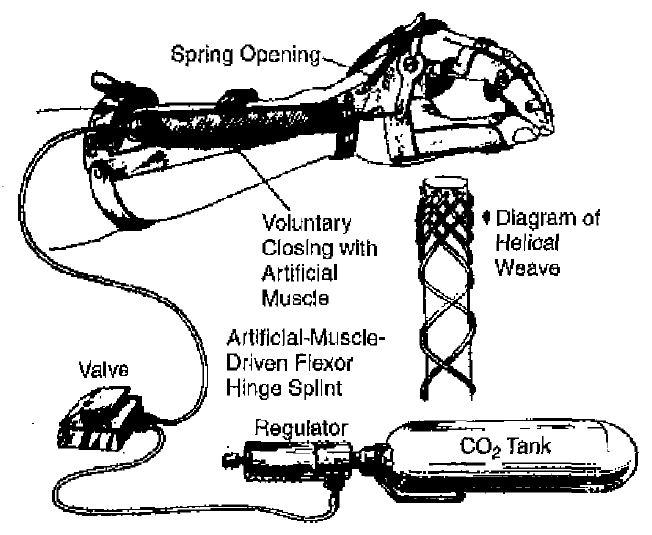
Pneumatic artificical muscle basic components [1]

Pneumatic artificical muscle contracting and relaxing
PAM has some disadvantages over electric motor actuator and in the same time some disadvantages. PAM benefits compliance property from the air compressability. PAM has high power-to-weight ratio and is capable to produce large force in short amount of time. On the other hand, PAM has drawback from its low controlabilty.
There are several types of PAMs. The two most known types are braided muscle —mostly known as McKibben muscle— and pleated muscle.
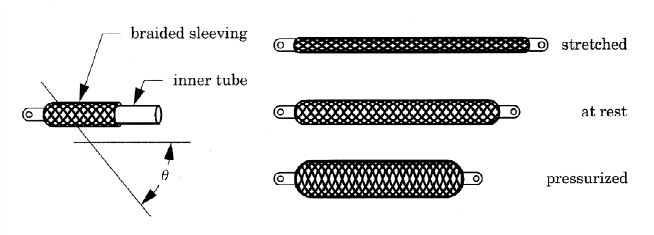

Different types of pneumatic artificial muscle actuator: McKibben muscle (left) and pleated muscle (right) [2]
McKibben muscle model
Muscle output force
McKibben muscles consist of internal rubber bladder surrounded by a braided mesh shell. When the internal bladder is pressurized and its volume increases, the braided thread angle will change due to the nonextensibility of the braided thread.
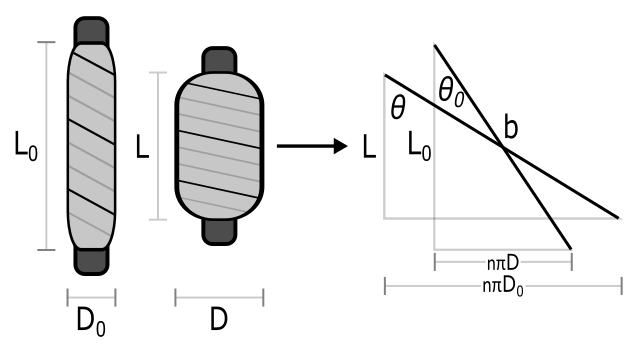
McKibben muscle geometry parameters during initial and pressurized state
\(\theta_0\) = initial braided thread angle [rad],
\(\theta\) = pressured braided thread angle [rad]
\(L_0\) = initial McKibben length [rad],
\(L\) = pressured McKibben length [rad]
\(D_0\) = initial McKibben diameter [m],
\(D\) = pressured McKibben diameter [m]
Based on above parameter, we can create a new parameter \(\epsilon\) for the change in length with respect to initial length:
\[\epsilon = \frac{L_0 - L}{L} = \frac{\cos\theta_0 - \cos\theta}{\cos\theta_0}\]The relationship between output force and geometry parameters can be calculated as below [3].
\[F = \frac{\pi D_0^2 P}{4 \sin^2 \theta_0} (3 \cos^2\theta -1)\]where:
\(F\) = output force [N]
\(P\) = pressure [Pa]
Using the \(\epsilon\) parameter we defined previously, we can simplify the equation into:
\[F = \frac{\pi D_0^2}{4} P (\alpha (1-\epsilon)^2 - \beta)\]where:
\(\alpha = 3 / \tan^2\theta_0\) ,
\(\beta = 1 / \sin^2\theta_0\) , and
\(\epsilon = {(L_0 - L)}/{L_0}\)
Muscle compliance
Muscle stiffness of McKibben muscle can be determined as derrivative of produced force about muscle contraction [2]. Then, muscle compliance can be determined as an inverse of muscle stiffness. From the output force equation, we can derive the quation into:
\[C^{-1} = K = \frac{\delta F}{\delta (\Delta L)} = \frac{6\pi}{\cot^2 \theta_0} \frac{D_0^2}{L_0^2} P L\]where \(C\) is muscle compliance and \(K\) is muscle stiffness.
Applications of pneumatic artifical muscle
The application of pneumatic artifical muscle may vary from:
- rehabilition device
- exoskeleton
- musculoskeletal robot
Further survey on application of pneumatic artifical muscle can be checked from the reference [4].
References:
[1] Bertrand Tondu and Pierre Lopez. Modeling and control of mckibben artificial muscle robot actuators.
IEEE control systems, Vol. 20, No. 2, pp. 15–38, 2000.
[2] Frank Daerden and Dirk Lefeber. Pneumatic artificial muscles: actuators for robotics and automation.
European journal of mechanical and environmental engineering, Vol. 47, No. 1, pp. 11–21, 2002.
[3] Ching Ping Chou and Blake Hannaford. Measurement and modeling of mckibben pneumatic artificial muscles.
IEEE Transactions on Robotics and Automation, Vol. 12, No. 1, pp. 90–102, 1996.
[4] Andrikopoulos, Georgios, Georgios Nikolakopoulos, and Stamatis Manesis. A survey on applications of pneumatic artificial muscles.
2011 19th Mediterranean Conference on Control & Automation (MED), pp. 1439-1446. IEEE, 2011