Jacobian Matrix

Notes on Jacobian matrix in robotics.

Introduction

Jacobian matrix defines the relation between joint velocities and end-effector velocities.

Just like forward kinematics from the previous note, which calculates the end-effector positions from the joint angles, Jacobian matrix provides the end-effector velocities from joint angle velocities.

Here, we define the end-effector position as $\mathbf{x}$ and joint angle as $\mathbf{q}$.

Formally, a Jacobian is a set of partial derivatives:

$$\mathbf{J} = \frac{\partial \mathbf{x}}{\partial \mathbf{q}}$$

Or, if we manipulate a bit so $\mathbf{J} = \frac{\partial \mathbf{x}}{\partial \mathbf{q}} = \frac{\partial \mathbf{x}}{\partial \mathbf{t}} \frac{\partial \mathbf{t}}{\partial \mathbf{q}}$ , we can get

$$\dot{\mathbf{x}} = \mathbf{J} \dot{\mathbf{q}}$$

Then we know that the Jacobian defines the relation between the end-effector velocities and the joint angle velocities.

Linear Velocity Jacobian

The simplest Jacobian matrix provides the relation end-effector linear velocity (we can call it linear velocity Jacobian $\mathbf{J}_v$).

Let us write the equation for an $n$R planar robot (2D robot in $n$ joints).

The end-effector velocity is defined as

$$\dot{\mathbf{x}} = \mathbf{J} \dot{\mathbf{q}}$$ $${\begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix}}_{2\times1} = {\begin{bmatrix} J_{11} & \dots & J_{1n} \\ J_{21} & \dots & J_{2n} \end{bmatrix}}_{2\times n} {\begin{bmatrix} \dot{q_1} \\ \vdots \\ \dot{q_n} \end{bmatrix}}_{n\times 1}$$

From the equation above, we can see that for any joint $i$, the Jacobian for its end-effector has a dimension of ${2\times i}$ (in 2D space).

Full Jacobian Matrix

A full Jacobian matrix consists of linear velocity part and angular velocity part. Simply,

$$\mathbf{J} = \begin{bmatrix} \mathbf{J}_v \\ \mathbf{J}_{\omega} \end{bmatrix}$$

With $\mathbf{J}_v = \frac{\partial \mathbf{x}}{\partial \mathbf{q}}$ for the linear velocity part and $\mathbf{J}_{\omega} = \frac{\partial \mathbf{\omega}}{\partial \mathbf{q}}$ for the angular velocity part. $\mathbf{\omega}$ denotes the angular rotation of the end-effector.

Building the Jacobian Matrix

We have known that a linear velocity Jacobian is

$$\mathbf{J}_v = \frac{\partial \mathbf{x}}{\partial \mathbf{q}}$$

So, after we know the position of end-effector $\mathbf{x_i} = \begin{bmatrix} x_i \\ y_i \end{bmatrix}$ of a joint $i$, we can easily create the set of partial derivatives for the linear velocity Jacobian as:

$$\mathbf{J}_v = {\begin{bmatrix} \frac{\partial \mathbf{x_i}}{\partial \mathbf{q_1}} & \dots & \frac{\partial \mathbf{x_i}}{\partial \mathbf{q_i}} \\ \frac{\partial \mathbf{y_i}}{\partial \mathbf{q_1}} & \dots & \frac{\partial \mathbf{y_i}}{\partial \mathbf{q_i}} \end{bmatrix}}_{2 \times i}$$

The same method applies for the angular velocity Jacobian $\mathbf{J}_{\omega}$.

Canonical example: 2R robot

Let’s try with an example of a 2R robot.

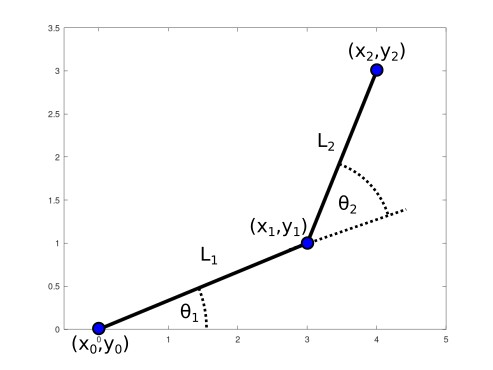
A planar 2-DOF serial link robot

From the previous note, using forward kinematics, we can get the position of end-effector of each joint $i$ as

$$\textbf{x}_1 = \begin{bmatrix} L_1 c_1 \\ L_1 s_1 \\ 1 \end{bmatrix}$$ $$\textbf{x}_2 = \begin{bmatrix} L_1 c_1 + L_2 c_{12} \\ L_1 s_1 + L_2 s_{12} \\ 1 \end{bmatrix}$$

With $c_{1} = cos(q_1)$, $s_{1} = sin(q_1)$, $c_{12} = cos(q_1+q_2)$, $s_{12} = sin(q_1+q_2)$, and $L_0 = 0$.

The linear velocity Jacobian can be calculated as:

$${\mathbf{J}_1}_v = \begin{bmatrix} \frac{\partial \mathbf{x_1}}{\partial \mathbf{q_1}}\\ \frac{\partial \mathbf{y_1}}{\partial \mathbf{q_1}} \end{bmatrix} = \begin{bmatrix} -L_1 s_1 \\ L_1 c_1 \\ 0 \end{bmatrix}$$ $${\mathbf{J}_2}_v = \begin{bmatrix} \frac{\partial \mathbf{x_2}}{\partial \mathbf{q_1}} & \frac{\partial \mathbf{x_2}}{\partial \mathbf{q_2}}\\ \frac{\partial \mathbf{y_2}}{\partial \mathbf{q_1}} & \frac{\partial \mathbf{y_2}}{\partial \mathbf{q_2}} \end{bmatrix} = \begin{bmatrix} -L_1 s_1 - L_2 s_{12} & -L_2 s_{12} \\ L_1 c_1 + L_2 c_{12} & L_2 c_{12} \\ 0 & 0 \end{bmatrix}$$

(Note that we define the position as a ${3\times 1}$ matrix here. So, the Jacobian matrix is ${3\times i}$ matrix)