Orientation representation for a rigid body in a 3D space.

Introduction

In general, a rigid body in a 3D space has six degrees of freedom: three translational and three rotational. At a given time, a rigid body has a pose, defined as position and orientation, with respect to a reference frame. A transformations represents the changes from a pose to another pose. Basic transformations include translation and rotation.

For position and translation, the representation is based on the chosen coordinates system: Cartesian coordinates, or Polar coordinates. Cartesian coordinates system is the common coordinates to represent the translation. For further information about coordinates system, www.euclideanspace.com has a broad description and examples [1].

For orientation and rotation, there are several representations available [2][3].

  1. Rotation matrices
    • :o: The general representation of a relative orientation.
    • :x: Not compact
    • :x: Not intuitive
  2. Euler angles
    • :o: The most compact and intuitive (minimal representation)
    • :x: Hass issue on gimbal lock!
    • :x: Ambiguity –> need to determine axis
  3. Quaternions
    • :o: No ambiguity (define a single unique orientation)
    • :o: Avoid gimbal lock
    • :o: Easier to compute
    • :x: Not intuitive

Further explanations are also available on Wikipedia [4].

1. Rotation matrices

A rotation by \(\alpha\) about X-axis: \(R_{x}(\alpha) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \\ \end{bmatrix}\)

A rotation by \(\beta\) about Y-axis: \(R_{y}(\beta) = \begin{bmatrix} cos(\beta) & 0 & -sin(\beta) \\ 0 & 1 & 0 \\ sin(\beta) & 0 & cos(\beta) \\ \end{bmatrix}\)

A rotation by \(\gamma\) about Z-axis: \(R_{z}(\gamma) = \begin{bmatrix} cos(\gamma) & -sin(\gamma) & 0 \\ sin(\gamma) & cos(\gamma) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\)

Compound rotations

Compound rotations are the multiplication of rotation matrices.

\[R(xyz,\alpha,\beta,\gamma) = R(x,\alpha) R(y,\beta) R(z,\gamma)\]

2. Euler angles

Euler angles are a minimal representation of a compound rotations, describing the sequence of rotations about the axes. For a 3D space, there are 12 Euler angles conventions:

XYX YXY ZXY
XYZ YXZ ZXZ
XZX YZX ZYX
XZY YZY ZYZ

NOTE: It is actually X-Y’-Z” instead of X-Y-Z, because the rotation depends on the new frame resulted from the first rotation. Here, it is written as XYZ for simplification.

Each robot maker has their own Euler angle conventions [5], for example:

Robot makers Euler Angle convention
FANUC, Motoman, KUKA XYZ
ABB ZYX
Kawasaki, Omron ZYZ

Forward Mapping

Forward mapping calculates the given Euler angles to the resulting rotation matrix.

Inverse Mapping

Inverse mapping calculates the given orientation matrix, to the Euler angles resulting the orientation.

Roll, Pitch, Yaw

In aircraft, the principal axes are commonly called roll, pitch, and yaw (or may also be called RPY angles).

Fig.1 Roll, Pitch, Yaw [6]

The convention used in RPY angles is a ZYX convention. The forward mapping of RPY angles is as follows, with \(\alpha\) as roll, \(\beta\) as pitch, \(\gamma\) as yaw.

\[R(RPY,\alpha,\beta,\gamma) = R(z,\gamma) R(y,\beta) R(x,\alpha)\]

Heading, Attitude, Bank

Another terms for Euler angles in aircraft are heading, attitude, and bank. Heading is for the angle applied first, attitude is for the angle applied second, and bank is for the angle applied third.

Since RPY angles follow ZYX convention, heading-attitude-back is equal to yaw-pitch-roll.

3. Quaternion

Quaternions represent the orientation using a number system that extends the complex numbers.

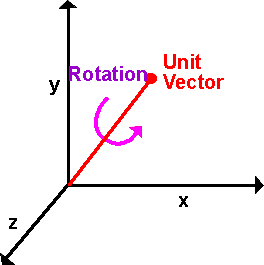
Fig.2. Rotation around an axis [7]

Consider the following rotation around an axis [7]. The rotation can be represented as a rotation \(\theta\) around the Euclidean vector \(\hat{u}\), with:

\[\hat{u} = u_x \hat{i} + u_y \hat{j} + u_z \hat{k}\]

Quaternion represent this rotation in a form of:

\[q = w + x \hat{i} + y \hat{j} + z \hat{k}\]

where

\[q = cos(\frac{\theta}{2}) + ( u_x \hat{i} + u_y \hat{j} + u_z \hat{k} ) sin(\frac{\theta}{2})\]

Samples in 90 degree steps

The following shows the sample rotations in 90 degree steps [8][9].

1. Applying heading as the first rotation.

$$ R = R(z,0) R(y,0) R(x,0) $$ $$ q = 1 + 0 \hat{i} + 0 \hat{j} + 0 \hat{k} $$ $$ R = R(z,90) R(y,0) R(x,0) $$ $$ q = 0.707 + 0 \hat{i} + 0.707 \hat{j} + 0 \hat{k} $$ $$ R = R(z,180) R(y,0) R(x,0) $$ $$ q = 0 + 0 \hat{i} + 1 \hat{j} + 0 \hat{k} $$ $$ R = R(z,-90) R(y,0) R(x,0) $$ $$ q = 0.707 + 0 \hat{i} - 0.707 \hat{j} + 0 \hat{k} \\ q = -0.707 + 0 \hat{i} + 0.707 \hat{j} + 0 \hat{k} $$

2. Applying attitude as the second rotation.

2.1 Attitude +90 degree.

$$ R = R(z,0) R(y,90) R(x,0) $$ $$ q = 0.707 + 0 \hat{i} + 0 \hat{j} + 0.707 \hat{k} $$ $$ R = R(z,90) R(y,90) R(x,0) $$ $$ q = 0.5 + 0.5 \hat{i} + 0.5 \hat{j} + 0.5 \hat{k} $$ $$ R = R(z,180) R(y,90) R(x,0) $$ $$ q = 0 + 0.707 \hat{i} + 0.707 \hat{j} + 0 \hat{k} $$ $$ R = R(z,-90) R(y,90) R(x,0) $$ $$ q = 0.5 - 0.5 \hat{i} - 0.5 \hat{j} + 0.5 \hat{k} $$

2.2 Attitude -90 degree.

$$ R = R(z,0) R(y,-90) R(x,0) $$ $$ q = 0.707 + 0 \hat{i} + 0 \hat{j} - 0.707 \hat{k} \\ q = -0.707 + 0 \hat{i} + 0 \hat{j} + 0.707 \hat{k} $$ $$ R = R(z,90) R(y,-90) R(x,0) $$ $$ q = 0.5 - 0.5 \hat{i} + 0.5 \hat{j} - 0.5 \hat{k} $$ $$ R = R(z,180) R(y,-90) R(x,0) $$ $$ q = 0 - 0.707 \hat{i} + 0.707 \hat{j} + 0 \hat{k} \\ q = 0 + 0.707 \hat{i} - 0.707 \hat{j} + 0 \hat{k} $$ $$ R = R(z,-90) R(y,-90) R(x,0) $$ $$ q = 0.5 + 0.5 \hat{i} - 0.5 \hat{j} - 0.5 \hat{k} $$

3. Applying bank as the second rotation. (Not as the third rotation.)

3.1 Bank +90 degree.

$$ R = R(z,0) R(y,0) R(x,90) $$ $$ q = 0.707 + 0.707 \hat{i} + 0 \hat{j} + 0 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,90) $$ $$ q = 0.5 + 0.5 \hat{i} + 0.5 \hat{j} + 0.5 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,90) $$ $$ q = 0 + 0 \hat{i} + 0.707 \hat{j} - 0.707 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,90) $$ $$ q = 0.5 + 0.5 \hat{i} - 0.5 \hat{j} + 0.5 \hat{k} $$

3.2 Bank +180 degree.

$$ R = R(z,0) R(y,0) R(x,180) $$ $$ q = 0 + 1 \hat{i} + 0 \hat{j} + 0 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,180) $$ $$ q = 0 + 0.707 \hat{i} + 0 \hat{j} - 0.707 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,180) $$ $$ q = 0 + 0 \hat{i} + 0 \hat{j} + 1 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,180) $$ $$ q = 0 + 0.707 \hat{i} + 0 \hat{j} + 0.707 \hat{k} $$

3.3 Bank -90 degree.

$$ R = R(z,0) R(y,0) R(x,-90) $$ $$ q = 0.707 - 0.707 \hat{i} + 0 \hat{j} + 0 \hat{k} \\ q = -0.707 + 0.707 \hat{i} + 0 \hat{j} + 0 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,-90) $$ $$ q = 0.5 - 0.5 \hat{i} + 0.5 \hat{j} + 0.5 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,-90) $$ $$ q = 0 + 0 \hat{i} + 0.707 \hat{j} + 0.707 \hat{k} $$ $$ R = R(z,0) R(y,0) R(x,-90) $$ $$ q = 0.5 - 0.5 \hat{i} - 0.5 \hat{j} + 0.5 \hat{k} $$

References:

[1] https://www.euclideanspace.com/maths/geometry/space/coordinates/index.htm

[2] https://www.euclideanspace.com/physics/kinematics/orientation/index.htm

[3] https://en.wikibooks.org/wiki/Robotics_Kinematics_and_Dynamics/Description_of_Position_and_Orientation

[4] https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation

[5] https://mecademic.com/insights/academic-tutorials/space-orientation-euler-angles/

[6] https://en.wikipedia.org/wiki/Aircraft_principal_axes

[7] https://www.euclideanspace.com/maths/geometry/rotations/axisAngle/index.htm

[8] https://www.euclideanspace.com/maths/algebra/realNormedAlgebra/quaternions/transforms/examples/index.htm

[9] https://www.euclideanspace.com/maths/geometry/rotations/euler/examples/index.htm

Bonus:

Good visualization for quaternions: https://quaternions.online/