Muscle synergies as a control method on musculoskeletal robots
Review on muscle synergies from neuroscience as a candidate for control method on musculoskeletal robots.
Overview
Musculoskeletal robots with pnematic artifical muscles (PAMs) has drawback on low controlability for position (posture) control. Since a musculoskeletal humanoid robot basically mimics human muscular system, how human muscles are coordinated in synergies might give an insight for a better method on controlling PAMS on musculoskeletal robot.
Muscle synergies
Muscle activation pattern on group of muscles on specific task are handled by the Central nervous system (CNS) control in some cpooordination called muscle synergy, or M-modes [1]. Previous researches have shown various of motor tasks can be described in muscle synergies: postural task on cat [2]; swimming and jumping on frog [3]. By using muscle synergies, Ting has shown that high complexity task or behavior (many muscles and direction) can be reduced to low dimensional patterns [2]. From this result, we can imply that CNS select group of muscles needed for completing tasks with muscle synergy as the balance ratio between the active muscles. Because of difference in the position of the muscles, the activation of each muscles affect the success rate of the task. Therefore, muscle synergy come with activation coefficient and synchronize the activation of each muscle and represent the muscle activation pattern in spatial characteristics.
The muscle activation pattern on each muscle consists of linear combination of the muscle synergies, and takes form
\[\boldsymbol {M} = \sum_{i=1}^n c_i \boldsymbol {W}_i = c_1 \boldsymbol {W}_1 + c_2 \boldsymbol {W}_2 + \dots + c_n \boldsymbol {W}_n \label{eq:synergy}\]where \(\textbf{M}\) is muscle activation pattern on each muscle, \(c_i\) is activation coefficient for each synergy i, and \(\textbf{W}_i\) is the vector specifying spatial pattern of muscle activity that defined by synergy i.
The identification of the muscle synergies can be done by using linear decomposition techniques, such as Principal Composition Analysis (PCA) and Nonnegative Matrix Factorization (NMF) [4]. Each of the techniques had shown the result on defining muscle synergies: postural body sway with M-modes by PCA [1] and postural responses with muscle synergies by NMF [2]. Based on these results, both PCA and NMF can be used to define muscle synergies. However Ting later compared PCA and NMF in several task and had shown that NMF is better on muscle synergies analysis based on variability accounted for (VAF), level of similarity between the actual and reconstructed signal [5].
Muscle synergies on human
From the result of muscle synergy on motor behaviors on animals, muscle synergies on human motor behavior become another subject to examine. Torres-Oviedo extracted the muscle synergies in human postural responses with perturbance from all direction and had shown that muscle synergies take place in postural control [6].
On the experiment, the human subjects are given perturbance while the electromyography (EMG) signal from 16 leg and lower-back muscles being recorded. Using NMF, the muscle synergies are extracted from the EMG data matrices. The extracted muscle synergies are used to reconstruct the EMG pattern. From the result, the reconstructed pattern EMG gives the same pattern with the original mean EMG response from the subjects. Therefore, it is clear that the muscle synergies have important role in defining muscle activation pattern on each muscle.
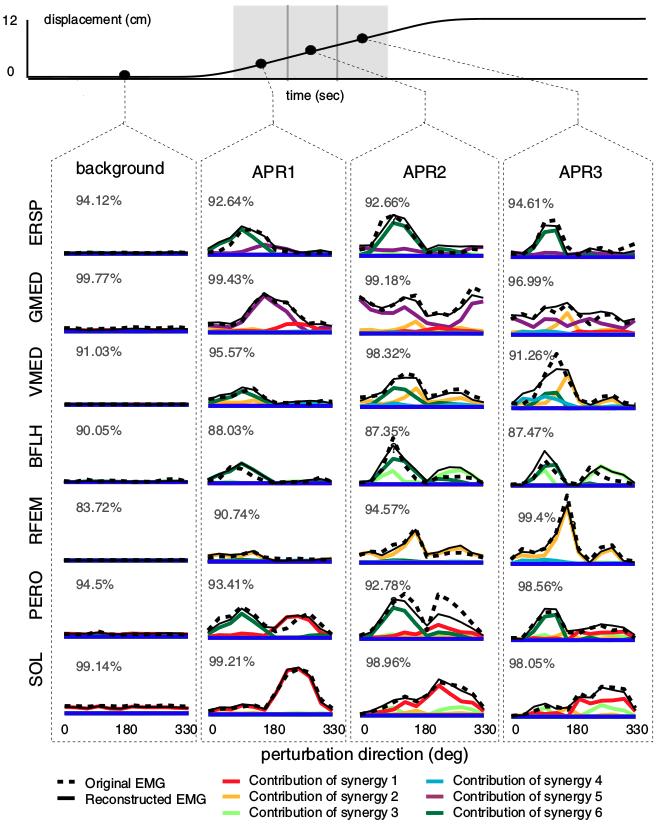
Reconstructed EMG pattern from muscle synergies giving the same tendency with the original EMG responses [6]
From this experiment, the muscle synergies extracted from EMG also cover pertubation for all direction, resulting in time-varying activation coefficients which are linear to the displacement due to the perturbation.
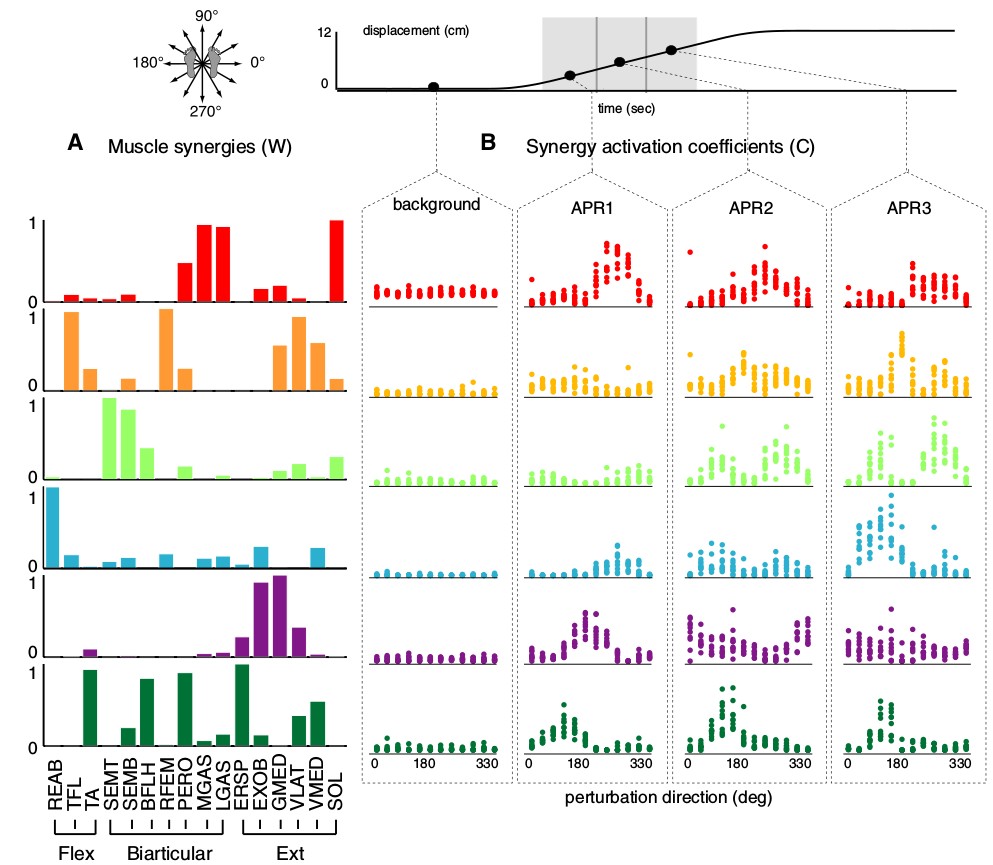
Muscle synergies and activation coefficient on postural with pertubances in all direction [6]
Using the same method, other researches are conducted for more advanced postural behavior on human: various type of postures, such as normal, narrow, wide, crouched, and one-leg stance [7]; nonstepping and stepping postural response behavior [8].
Muscle synergies on robotics
Several researches are conducted in musculoskeletal with purpose of generating robot locomotion, based on muscle synergies on human: walking [9]; running [10]; and pedaling [11] [12]. The result from walking and running tasks showed the same result between human and robot, but these researches only concern on the leg posture and gait cycle, not on the contacts between the robot leg and the ground. The pedaling task was chosen since pedaling is one of the simplest lower-limb locomotion without failure state and it involves interaction with the environment.
The aboves works used the same experiment method:
- Measurement of EMG sinals on human subject on a specific task.
- Extraction of muscle synergies using PCA.
- Calculation of equilibrium joint angle as common parameter between human and rbot in terms of A-A ratio and A-A sum.
- Air pressure (for PAM) setting based on A-A ratio and A-A sum.
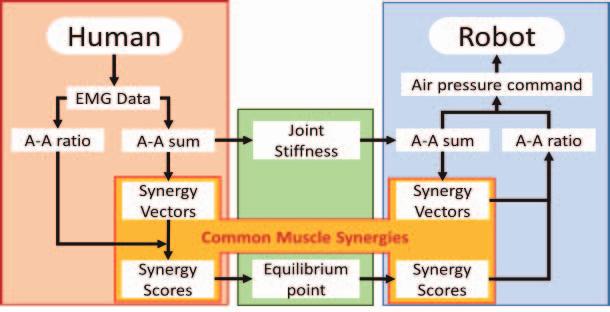
Muscle synergies-based control method on musculoskeletal robot [12]
Ariga proposed novel control method for PAM with agonist-antagonist configuration using equilibrium point (EP) joint angle in terms of A-A ratio and A-A sum [13]. The proposed control method is based on a modified model of McKibben PAM model proposed by Chou [14]. Based on the model proposed by Chou, the force produced by the agonist-antagonist PAM can be derived into relation with the equilibrium joint angle.
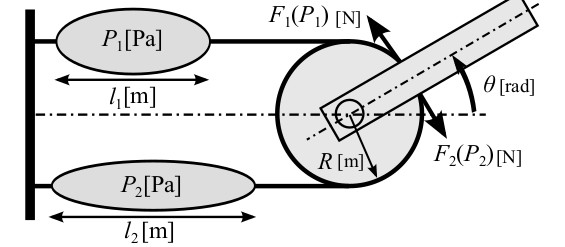
Agonist-antagonist muscle configuration [13]
Since \(F_1 = F_2\), Ariga derived the relation between agonis-antagonist muscle in term of A-A ratio r, and A-A sum a,
\[r = \frac{\hat{P_1}}{\hat{P_1} + \hat{P_2}}\] \[a = \hat{P_1} + \hat{P_2}\]where r show the ratio on pressure of one PAM to total pressure of two PAMs a.
The linear relation between r and equilibrium point \(\theta\) are
\[\theta = C (r - \frac{1}{2})\]In pedaling task [12], Watanabe use this A-A ratio and A-A sum in analogy between human and musculoskeletal robot.
In robot:
\[r_{Robot} = \frac{\hat{P_1}}{\hat{P_1} + \hat{P_2}}\] \[a_{Robot} = \hat{P_1} + \hat{P_2}\]whereas in human:
\[r_{Human} = \frac{m_1}{m_1 + m_2}\] \[a_{Human} = m_1 + m_2\]where P is the pressure for PAM and m is the muscle activity on one muscle.
By using A-A ratio and A-A sum as physical properties of muscle synergies, it was shown that muscle synergies can be used for controlling PAM, and resulting in capable of doing various task the same with what human do. With the result, implementation of muscle synergies is shown as an alternative contol method for musculoskeletal humanoid robot with redundant muscles.
Discussion
The problem of controllability of pneumatic artificial muscles may lead to new approach on controlling the actuator on robot. Musculoskeletal humanoid robot, which is designed similar to human structure, may also mimic not only the morphology (structure and forms), but also the physiology (functionality) of human. Since PAM is used based on human muscle, the way Central Nervous System controls the muscle activation may give a new perspective on how the robot control the PAM. Therefore, muscle synergies approach might be suitable for implementation on a musculoskeletal robot.
One problem for implementing the muscle synergies is the dependency on human subject experiment for acquiring EMG data. This problem might be difficult to tackle, since the design of the musculoskeletal robot and the muscle selection affect the EMG data needed. There are some possible solutions:
- Self measurement of EMG data for the chosen muscles
- Muscle selection based on the available EMG data on neurophysiology researches
- EMG data reconstruction for the chosen muscles from muscle synergies derived from available EMG data.
References:
[1] V. Krishnamoorthy, M. Latash, J. Scholz, et al., “Muscle synergies during shifts of the center of pressure by standing persons” Experimental Brain Research, vol. 152, no. 3, pp. 281–292, 2003.
[2] L. H. Ting and J. M. Macpherson, “A limited set of muscle synergies for force control during a postural task,” Journal of neurophysiology, vol. 93, no. 1, pp. 609–613, 2005.
[3] V. C. Cheung, A. d’Avella, M. C. Tresch, et al., “Central and sensory contributions to the activation and organization of muscle synergies during natural motor behaviors,” Journal of Neuroscience, vol. 25, no. 27, pp. 6419–6434, 2005.
[4] D. D. Lee and H. S. Seung, “Learning the parts of objects by non-negative matrix factorization,” Nature, vol. 401, no. 6755, pp. 788–791, 1999.
[5] L. H. Ting and S. A. Chvatal, “Decomposing muscle activity in motor tasks,” Motor Control Theories, Experiments and Applications. Oxf. Univ. Press, New York, pp. 102v–138, 2010.
[6] G. Torres-Oviedo and L. H. Ting, “Muscle synergies characterizing human postural responses,” Journal of Neurophysiology, vol. 98, no. 4, pp. 2144–2156, 2007.
[7] G. Torres-Oviedo and L. H. Ting, “Subject-specific muscle synergies in human balance control are consistent across different biomechanical contexts,” Journal of Neurophysiology, vol. 103, no. 6, pp. 3084–3098, 2010.
[8] S. A. Chvatal, G. Torres-Oviedo, S. A. Safavynia, et al., “Common muscle synergies for control of center of mass and force in nonstepping and stepping postural behaviors,” Journal of Neurophysiology, vol. 106, no. 2, pp. 999–1015, 2011.
[9] H. Hirai, K. Matsui, T. Iimura, et al., “Modular control of limb kinematics during human walking,” in IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), 2010, pp. 716–721.
[10] T. Iimura, K. Inoue, H. T. Pham, et al., “A preliminary experiment for transferring human motion to a musculoskeletal robot-decomposition of human running based on muscular coordination,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2011, pp. 4496–4501.
[11] T. Oku, K. Inoue, T. H. Pham, et al., “Analysis of muscle coordination in human pedaling and implementation with a musculoskeletal robot,” in IEEE-RAS International Conference on Humanoid Robots (Humanoids), 2012, pp. 606–611.
[12] E. Watanabe, T. Oku, H. Hirai, et al., “Exploiting invariant structure for controlling multiple muscles in anthropomorphic legs: An inspiration from electromyography analysis of human pedaling,” in IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), 2015, pp. 88–93.
[13] Y. Ariga, H. T. Pham, M. Uemura, et al., “Novel equilibrium-point control of agonist-antagonist system with pneumatic artificial muscles,” in IEEE International Conference on Robotics and Automation (ICRA), 2012, pp. 1470–1475.
[14] C. P. Chou and B. Hannaford, “Measurement and modeling of mckibben pneumatic artificial muscles,” IEEE Transactions on Robotics and Automation, vol. 12, no. 1, pp. 90–102, 1996.